Case 02 — Rigid beam supported by elastic vertical posts
Verification of vertical displacement of a rigid beam supported by two vertical elastic posts with different stiffness. The system consists of a rigid horizontal beam resting on steel and aluminum posts and subjected to a concentrated vertical load. This verification case validates the correct implementation of axial bar elements with different material stiffness and their interaction with a rigid beam element in the RodX finite element solver.
Description
A rigid horizontal beam is supported by two vertical elastic posts. The left post is made of steel, and the right post is made of aluminum. The beam itself is assumed to be rigid, while axial deformations occur only in the supporting posts. A vertical concentrated load is applied to the beam at an intermediate point between the supports.
Determine:
- Vertical displacement of the rigid beam at the load application point.
Structural scheme
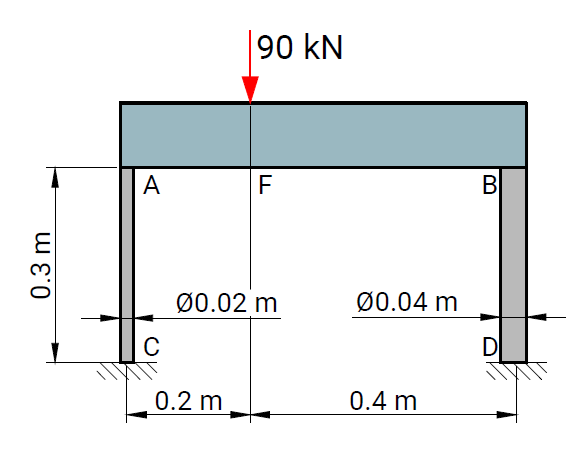
Geometry, boundary conditions, and load applications used in the verification model.
Model parameters
| Parameter | Value |
|---|---|
| Element type | Beam elements |
| Material | Steel, Aluminum |
| Young's modulus | 2.0 × 10⁸ kN/m², 7.0 × 10⁷ kN/m² |
| Diameter | 0.02 m, 0.05 m |
| Boundary conditions | Fixed supports at the bases of both posts |
| Loads | Vertical concentrated load of 90 kN applied to the rigid beam |
Numerical results
Displacements

Table results from RodX

Comparison
| Node | Analytical solution | RodX | Midas/Civil |
|---|---|---|---|
| Δy(A) | -0.286 | -0.286 | -0.286 |
| Δy(F) | -0.225 | -0.225 | -0.225 |
| Δy(B) | -0.102 | -0.102 | -0.102 |
The numerical results obtained with RodX are in agreement with the analytical solution and reference FEA results.
Reference
- Hibbeler, R. C. Mechanics of Materials, 10th Edition (SI Units), Pearson Education, 2017, Example 4.3, p. 149.