These verification cases demonstrate the accuracy of RodX calculations by comparing results against analytical solutions, classical benchmark problems, and industry-recognized FEA software. This section presents a structured set of verification cases used to validate the RodX 2D finite element solver.
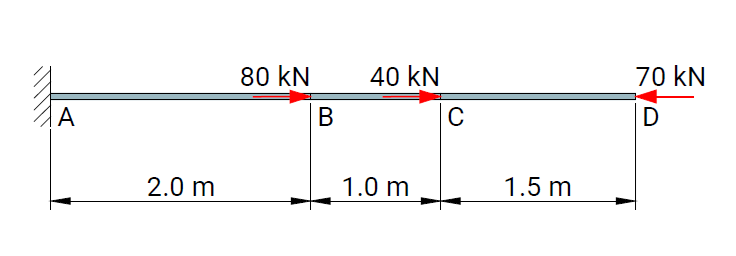
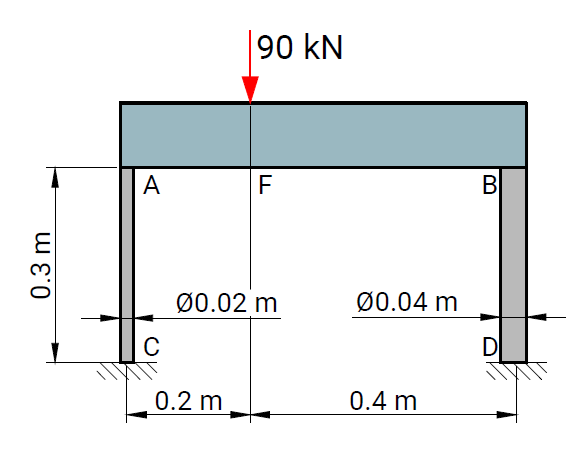
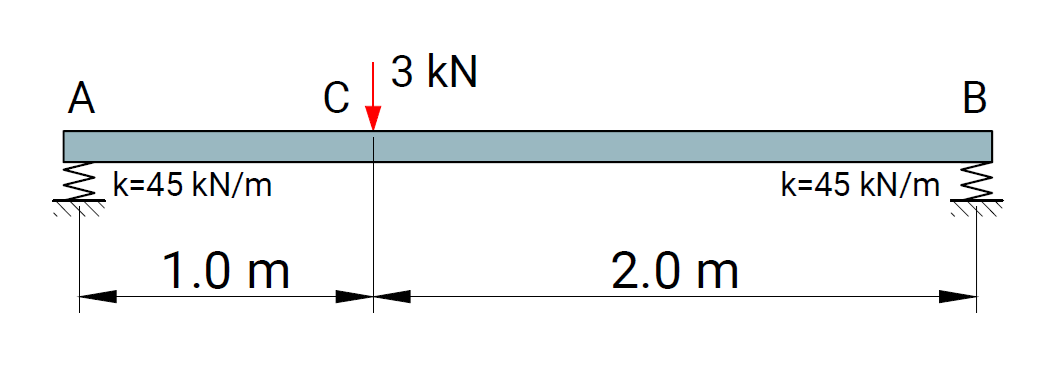
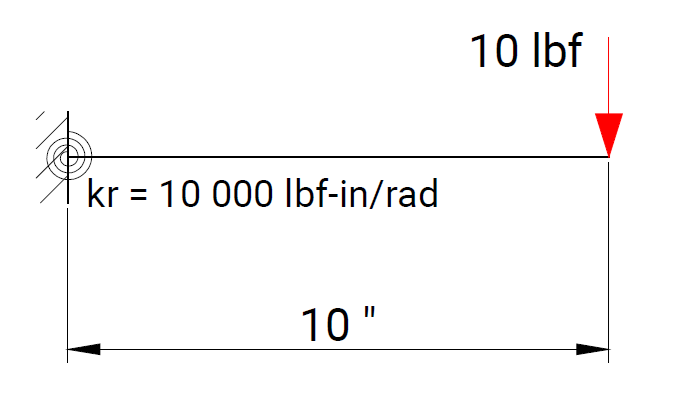
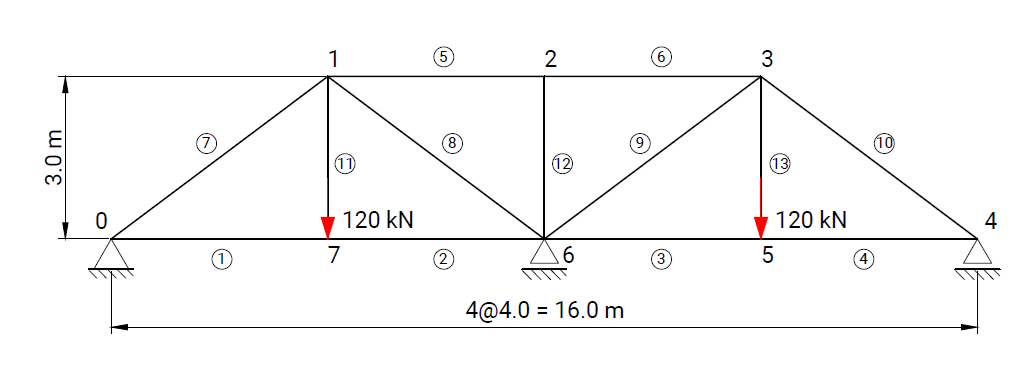
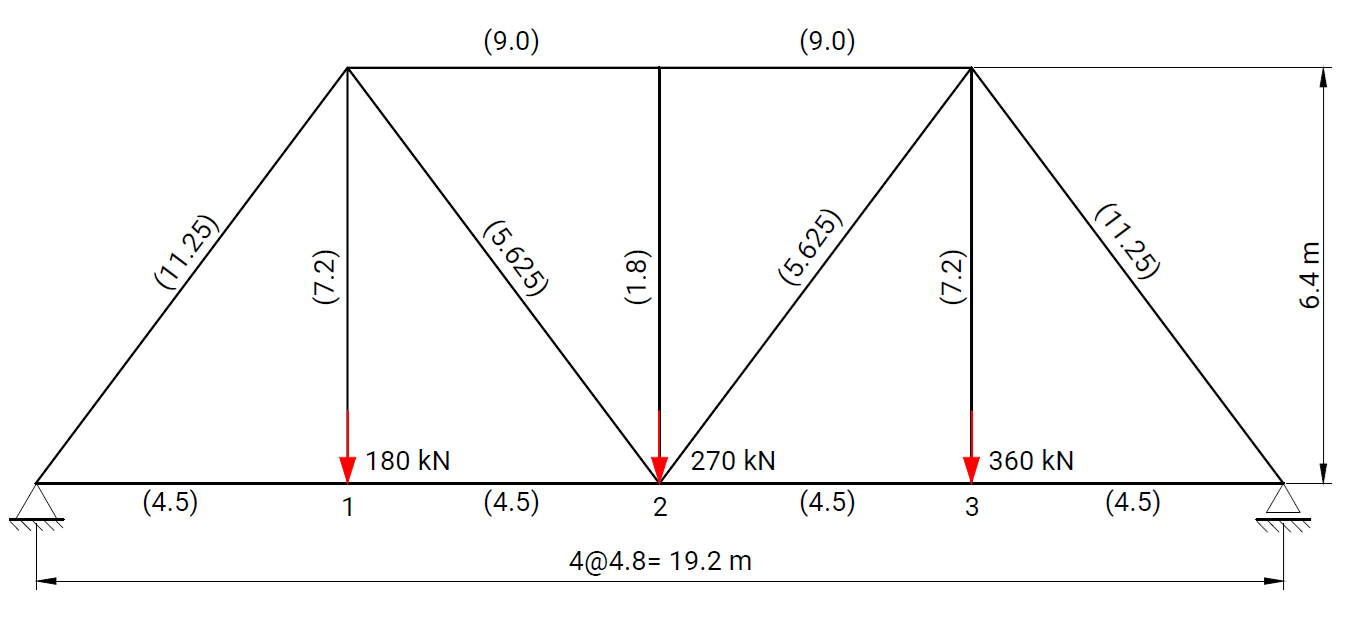
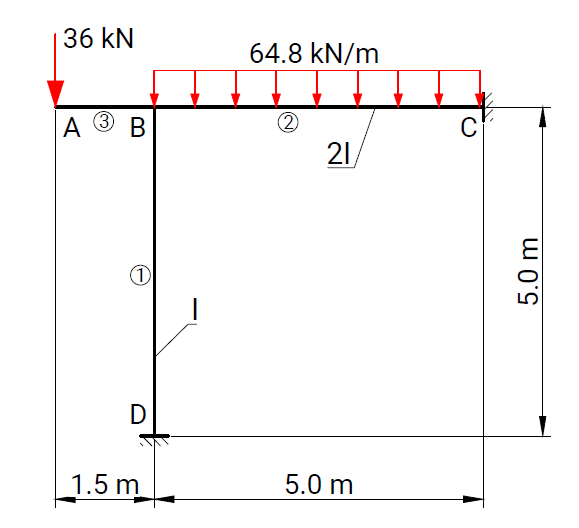
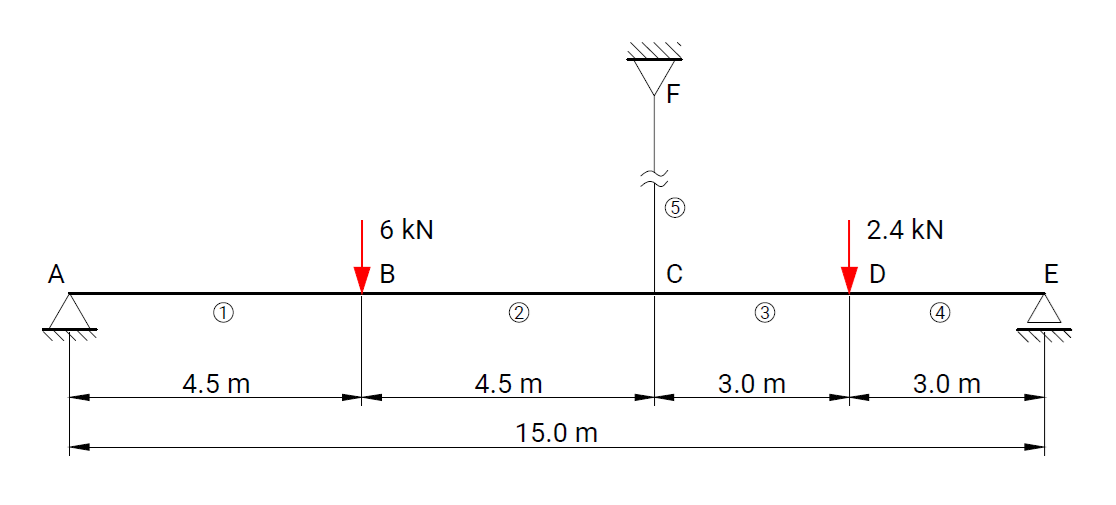
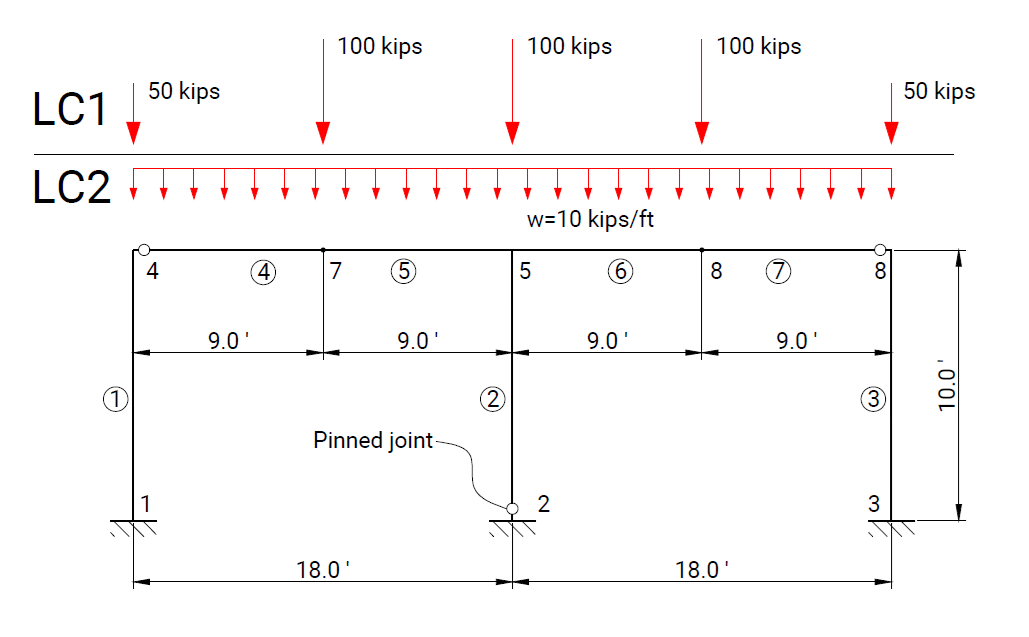
The objective of the verification process is to ensure the reliability of results produced by the computational solver and by the RodX interpretation layer for all element types and boundary conditions available in the platform.
Each verification case is based on a well-defined structural scheme taken from widely recognized and authoritative textbooks on structural analysis and strength of materials. The presented problems cover the full range of supported modeling features, including beam and truss elements, hinges, elastic supports, and various boundary condition configurations.
For each case, numerical results obtained with RodX are compared not only with analytical solutions, but also with results from equivalent models solved using industry-recognized finite element analysis (FEA) software. The comparison includes nodal displacements, internal forces, reaction forces, and the qualitative shape of force diagrams. Differences in the orientation of bending moment and shear force diagrams may occur and are attributed to variations in sign convention.
Verification of axial displacements for a prismatic steel bar subjected to multiple concentrated axial forces. The bar is fixed at one end and loaded at intermediate nodes along its length. Numerical results obtained with RodX are compared with analytical solutions and results from industry-recognized FEA software.
Verification of vertical displacement of a rigid beam supported by two vertical elastic posts with different stiffness. The system consists of a rigid horizontal beam resting on steel and aluminum posts and subjected to a concentrated vertical load. This verification case validates the correct implementation of axial bar elements with different material stiffness and their interaction with a rigid beam element in the RodX finite element solver.
Verification of vertical displacement of a steel beam supported by two identical vertical elastic springs. A concentrated vertical load is applied at an intermediate node along the beam span. This verification case validates the correct implementation of vertical elastic supports (spring elements) and their interaction with beam elements in the RodX finite.
A cantilever beam of finite length is subjected to a concentrated vertical load applied at its free end. The fixed end of the beam is supported by a rotational spring with a specified rotational stiffness. Vertical displacement and rotation at the free end are evaluated. This verification case validates the correct implementation of rotational spring supports and their influence on displacements and rotations in beam elements.
A symmetrical planar truss structure is subjected to vertical loads applied at selected joints. The structure is supported at both ends and modeled using truss elements only. This verification case validates the correct calculation of internal axial forces in truss elements subjected to symmetrical vertical loading.
A planar truss structure is subjected to multiple vertical loads applied at intermediate joints. The geometry of the truss and cross-sectional areas of the members are defined as shown in the reference scheme. The horizontal and vertical displacements of joint L3 are evaluated. This verification case validates the accuracy of nodal displacement calculations in truss elements, including both horizontal and vertical displacements of joints.
A rigid planar frame is subjected to a concentrated vertical load applied at joint A and a uniformly distributed load acting along the horizontal beam. The frame consists of a vertical column and a horizontal beam with different flexural stiffness. Bending moments at selected sections of the frame are evaluated. This verification case validates the calculation of bending moments in frame elements subjected to combined concentrated and distributed loading.
A timber beam is supported at both ends and subjected to two vertical concentrated loads. At an intermediate point, the beam is connected to a vertical steel hanger rod anchored to an overhead support. The vertical displacement of the connection point, support reactions, and axial force in the hanger are evaluated. This verification case validates the interaction between beam and truss elements in a composite structural system, including the correct calculation of displacements, support reactions, and axial force in a hanger rod.
A two-dimensional frame structure is subjected to vertical static loads, including concentrated nodal forces and a uniformly distributed load. The frame consists of two vertical columns connected by a horizontal beam and includes pinned connections at intermediate nodes. Shear force and bending moment diagrams are evaluated for two independent load cases. This verification case validates the correct modeling of internal hinges in frame elements and their influence on shear force and bending moment distributions.